Excitation energies at the SCF-level¶
In this tutorial we will look at the theory behind the calculation of excitation energies at the SCF-level, that is, either by time-dependent Hartree-Fock (TD-HF) or TD-DFT. The implementations in DIRAC are presented in [Bast2009].
Excitation energies \(\omega_m\) are found by solving the generalized eigenvalue problem
where the matrices \(E_0^{[2]}\) and \(S^{[2]}\) are the electronic Hessian and generalized metric, respectively. From their structure, it can be shown that solution vectors come in pairs
Transition moments associated with operator \(\hat{h}_{A}\) for transitions \(n\leftarrow0\) are generally calculated as
where appears solution vector \(\boldsymbol{X}_{+;n}^{\dagger}\) and property gradient \(\boldsymbol{E}_{A}^{[1]}\). The property gradient is given by
An important generalization above is that, in addition to Hermitian operators \(\hat{h}_{B}\) (\(\Theta_{hB}=+1\)), imposed by the tenets of quantum mechanics, we also allow anti-Hermitian ones (\(\Theta_{hB}=-1\)).
A key to computational efficiency is to consider a decomposition of solution vectors in terms of components of well-defined Hermiticity and time reversal symmetry. Using a pair of solution vectors \(\boldsymbol{X}_{+}\) and \(\boldsymbol{X}_{-}\), we may form Hermitian and anti-Hermitian combinations
The inverse relations therefore provide a separation of solution vectors into Hermitian and anti-Hermitian contributions
Further decomposition of each contribution into time-symmetric and time-antisymmetric parts give vectors that are well-defined with respect to both Hermiticity and time reversal symmetry
where
and the index overbar refers to a Kramers’ partner in a Kramers-restricted orbital set. The scalar product of such vectors is given by [Saue2002a]
and one may therefore distinguish three cases
One may show that Hermiticity is conserved when multiplying such a trial vector by the electronic Hessian, whereas it is reversed by the generalized metric. However, both the electronic Hessian and the generalized metric conserves time reversal symmetry. The implication is that the time-symmetric and time-antisymmetric components of a solution vector does not mix upon solving the generalized eigenvalue problem, and one can dispense with one of them. From a physical point of view, this can be understood from the observation that excited states can be reached through both time-symmetric and time-antisymmetric operators. In order to employ the quaternion symmetry scheme, we choose to work with the time-symmetric vectors. It follows from the above that their scalar product are either zero or real. In practice, a property gradient is therefore always contracted with the component of the solution vector having the same hermiticity, so that all transition moments are real.
Practical example¶
We consider the excitation \(1s_{1/2}\rightarrow 3p_{3/2}\,(\left|m_{j}\right|=1/2)\) of the magnesium atom. We limit attention to boson irrep \(B_{1u}\), corresponding to the symmetry of the \(z\) - coordinate (\(\Gamma_z\)). We work within the electric dipole approximation and from a character table of \(D_{2h}\) it is clear that we will only get non-zero transition moments from the z-component of the electric dipole operator.
We start from the menu file ed.inp
**DIRAC
.WAVE FUNCTION
.ANALYZE
.PROPERTIES
**INTEGRALS
*READIN
.UNCONT
**WAVE FUNCTION
.SCF
*SCF
.CLOSED SHELL
6 6
**PROPERTIES
*EXCITATION ENERGIES
.PRINT
10
.OCCUP
1
.VIRTUAL
6
.ANALYZE
! Excitations s -> p
.EXCITATION ! B1u
5 1
**ANALYZE
.MULPOP
*MULPOP
.VECPOP
1..oo
1..oo
**MOLECULE
*BASIS
.DEFAULT
dyall.ae2z
**END OF
and the xyz-file Mg.xyz
1
Mg 0.0D0 0.0D0 0.0D0
and run our calculation using:
pam --inp=ed --mol=Mg.xyz --get "DFCOEF PAMXVC"
We are keeping some file for later use, see below. It can be seen in the menu file ed.inp that excitations are only allowed from the first gerade orbital (\(1s_{1/2}\)) to the sixth ungerade one (\(3p_{3/2,1/2}\)). The nature of these orbitals can be seen from the Mulliken population analysis in the output.
We have increased the print level significantly in order to be able to look a bit under the hood. Let us first look at the property gradient
The matrix element \(g_{ai}\) may be written as
and similar for \(g_{a\overline{i}}\). For present purposes it suffices to think in terms of 2-component spinors. Since \(s_{1/2}\) and \(p_{3/2}\) have opposite parity, they will in the conventions of DIRAC have different symmetry structures
In addition we have to remember the relation between Kramers partners
In terms of symmetry the orbital distributions are
In the present case the operator symmetry is \(\Gamma_{z}\). Since the integrand of the matrix element has to be totally symmetric, we see that only the imaginary part of \(g_{ai}\) will be non-zero; the partner element \(g_{a\overline{i}}\) is strictly zero. The generally complex gradient elements are combined into a quaternion one
and, indeed, when we look in the output we find
Output from GPGET
-----------------
* Gradient (e-e) of property EpolL01X00Y00Z01
*** A imag part ***; NROW,NCOL,LRQ,LCQ: 1 1 1 1
Column 1
1 -0.00682451
==== End of matrix output ====
Here the notation EpolLnlXnxYnyZnz refers to a Cartesian electric multipole operator \(\hat{Q}^{[nl]}=-ex^{nx}y^{ny}z^{nz};\quad nx+ny+nz=nl\). Since this is a time symmetric, Hermitian operator, it will be contracted with the Hermitian part of the solution vector. In this particular case we have only a single orbital rotation, and between two orbitals of positive energy, so the relevant part of the solution vector is
E+ part of solution vectors for 1 excitations:
* Vector nr. 1
*** A imag part ***; NROW,NCOL,LRQ,LCQ: 1 1 1 1
Column 1
1 0.35355084
==== End of matrix output ====
Searching in the output, we find the corresponding calculated transition moment
< 0 |EpolL01X00Y00Z01| 1 > = -4.8256194928E-03 a.u.,
which is easily seen to be \(2*0.35355084*-0.00682451\). (With respect to Eq.(3) a factor two seems to be missing; this is appears to be connected to the scaling of eigenvectors in subroutine XPPORD.)
We may proceed to visualize the transition moment density
as a radial distribution, that is
As preparation we first inspect the file PAMXVC of solution vectors
dirac 2074>rspread.x PAMXVC
Solution vectors found on file : PAMXVC
** Solution vector : PP EXCITATIONB1u Irrep: 5 Trev: 1
1 Type : E+ Freq.: 48.935572 Rnorm: 0.16E-13 Length: 1
2 Type : E- Freq.: 48.935572 Rnorm: 0.16E-13 Length: 1
We see that the Hermitian e-e part of the solution vector E+ is the first vector on the file, which therefore leads us to set up the input file length.inp as
**DIRAC
.PROPERTIES
**INTEGRALS
*READIN
.UNCONT
**WAVE FUNCTION
.SCF
*SCF
.CLOSED SHELL
6 6
**GRID
.ULTRAFINE
**PROPERTIES
*EXPECTATION VALUES
.ORBANA
.OPERATOR
'XXSECMOM'
.OPERATOR
'YYSECMOM'
.OPERATOR
'ZZSECMOM'
**VISUAL
.EDIPZ
PAMXVC 1
.RADIAL
0.0D0 0.0D0 0.0D0
10.0
500
.3D_INT
**MOLECULE
*BASIS
.DEFAULT
dyall.ae2z
**END OF
We now generate the radial distribution using:
pam --inp=length --mol=Mg.xyz --put "DFCOEF PAMXVC" --get "plot.radial.scalar=length.dat"
First we may note at the end of the output
The radial distribution integrates to: 4.8280356220858738E-003
and so we see that the radial distribution integrates to the value obtained in our previous calculation.
Next, with a suitable plotting program (I used xmgrace) we can visualize the radial distribution
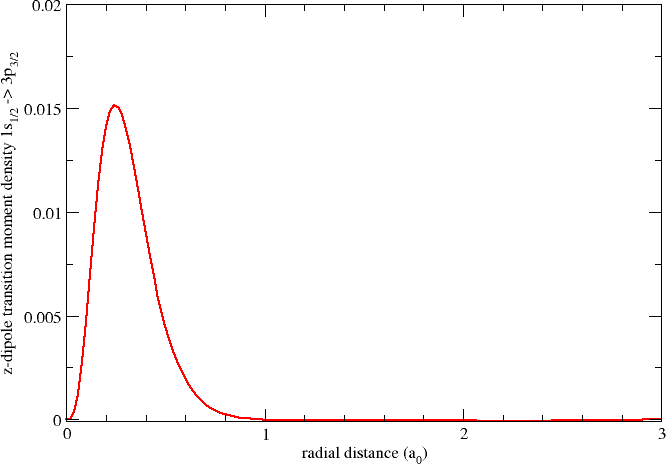
To get some idea of the extent of the z-electric dipole moment transition density associated with the \(1s_{1/2}\rightarrow 3p_{3/2}\,(\left|m_{j}\right|=1/2)\) transition, I have included in the input the calculation of orbital sizes as \(<r^2>^{1/2}=\left(<x^2>+<y^2>+<z^2>\right)^{1/2}\). Extracting and using the data from the output I obtain the following table (orbital labels are taken from the Mulliken analysis of the first calculation):
Sym. |
Orb. |
\(<x^2>\) |
\(<y^2>\) |
\(<z^2>\) |
\(<r^2>^{1/2}\) |
E1g |
1s 1/2; 1/2 |
0.008 |
0.008 |
0.008 |
0.151 |
E1g |
2s 1/2; 1/2 |
0.190 |
0.190 |
0.190 |
0.754 |
E1g |
3s 1/2; 1/2 |
4.106 |
4.106 |
4.106 |
3.510 |
E1u |
2p 1/2; 1/2 |
0.198 |
0.198 |
0.198 |
0.772 |
E1u |
2p 3/2; -3/2 |
0.240 |
0.240 |
0.120 |
0.774 |
E1u |
3p 3/2; 1/2 |
0.160 |
0.160 |
0.279 |
0.774 |
We see that the radial distribution peaks around 0.25 \(a_0\) which is slightly outside the size of the \(1s_{1/2}\) orbital.