Magnetizability density¶

In this tutorial we will plot the CGO magnetizability density of the water molecule. We will do this in two steps: first we will run the SCF and response calculation and save the DFCOEF and PAMXVC files, then we will restart from these and calculate the magnetizability density on a grid of points and write this into a cube file which can be opened by your favorite molecular visualization program (the author of this tutorial likes Avogadro).

Getting the wave function and the response vectors¶

Let us use the following molecule input (h2o.mol):

DIRAC


C   2    0
        1.    2
H    -1.4523499293         .0000000000         .8996235720
H     1.4523499293         .0000000000         .8996235720
LARGE BASIS cc-pVDZ
        8.    1
O      .0000000000        0.0000000000        -.2249058930
LARGE BASIS cc-pVDZ
FINISH

Together with a simple job input (magnetizability.inp):

**DIRAC
.WAVE FUNCTION
.PROPERTIES
**HAMILTONIAN
.DFT
 B3LYP
**WAVE FUNCTION
.SCF
**PROPERTIES
.MAGNETIZABILITY
*END OF INPUT

We can get the wave function with the following run script:

pam --inp=magnetizability.inp --mol=h2o.mol --get="DFCOEF PAMXVC"

After running the script you should see the files DFCOEF and PAMXVC in your submit directory.

And here is the magnetizability tensor:

            Total magnetizability tensor (au)
            ---------------------------------

                     Bx                  By                  Bz


Bx        -1.804460514289     -0.000000000000     -0.000000000001
By        -0.000000000000     -1.617444735515      0.000000000000
Bz        -0.000000000001     -0.000000000000     -1.709814652525

Plotting the magnetizability density¶

We will use the following run script to generate the cube file:

pam --inp=density.inp --mol=h2o.mol --put="DFCOEF PAMXVC" --get=plot.3d.cube

Together with the following job input (density.inp):

**DIRAC
#.WAVE FUNCTION
**HAMILTONIAN
.DFT
 B3LYP
**WAVE FUNCTION
.SCF
**VISUAL
.3D
 80 80 80
.BDIPX
 PAMXVC 1         # "paramagnetic" Bx response
.BDIPX
 PAMXVC 2         # "diamagnetic"  Bx response
.BDIPY
 PAMXVC 3         # "paramagnetic" By response
.BDIPY
 PAMXVC 4         # "diamagnetic"  By response
.BDIPZ
 PAMXVC 5         # "paramagnetic" Bz response
.BDIPZ
 PAMXVC 6         # "diamagnetic"  Bz response
.SCALE
 0.3333333        # we divide sum by 3 to get isotropic value
.3D_INT           # to double-check that density integrates to the magnetizability
*END OF INPUT

In the output we should verify that we integrate to the correct isotropic magnetizability:

   scalar              x-component         y-component         z-component

-0.1710573104E+01    0.0000000000E+00    0.0000000000E+00    0.0000000000E+00

Finally you can open plot.3d.cube with your favorite program and visualize the density. By selectively deactivating contributions in density.inp you can single out specific components or paramagnetic and diamagnetic contributions separately.

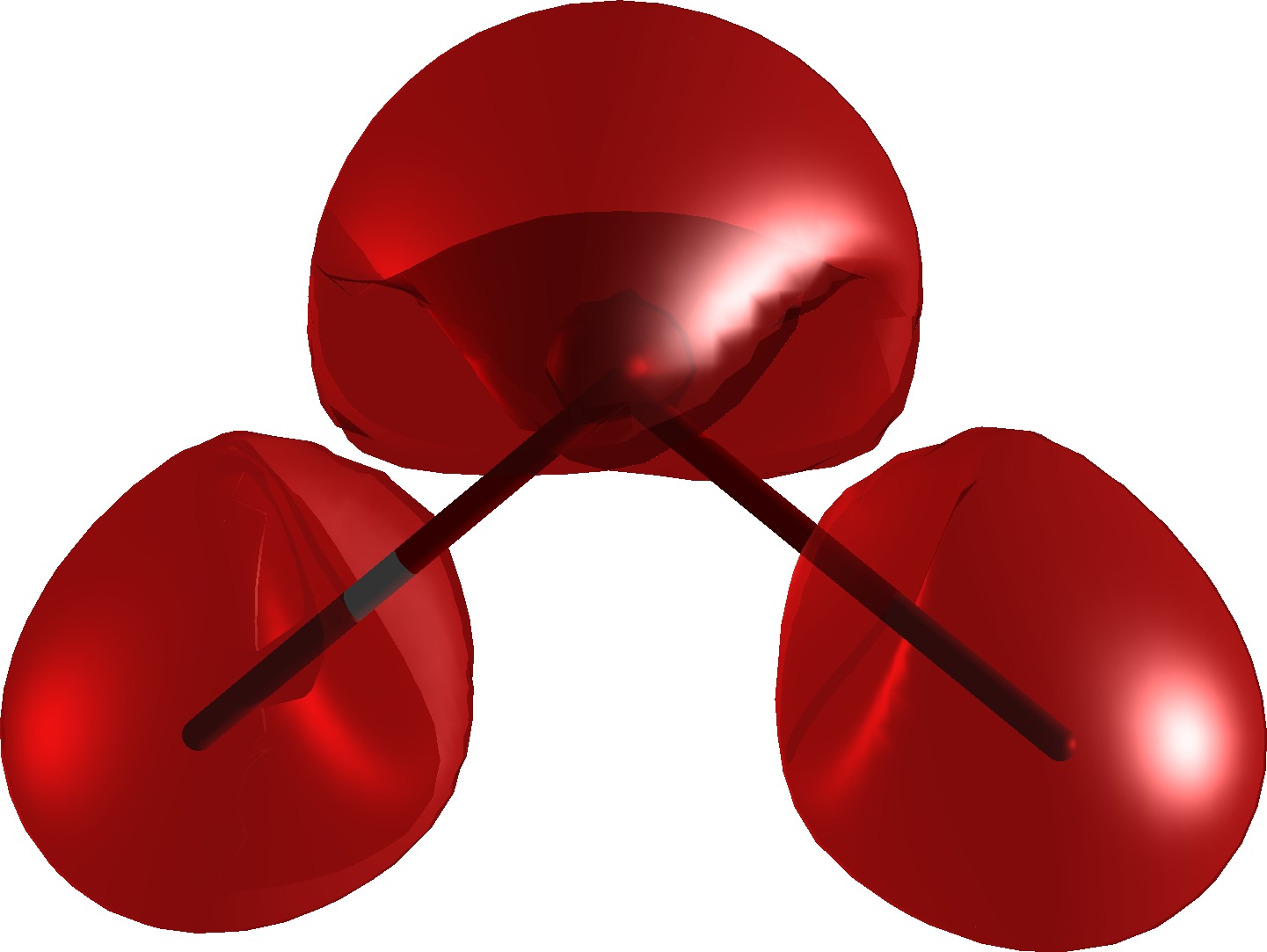
And this is how the magnetizability density of water looks (isosurface 0.04 a.u.):