1s core-ionization of N2 by TD-DFT¶
Introduction¶
We want to study the excitation of a 1s electron of the \(N_2\) molecule to an empty orbital. More precisely we shall look at the excitation of an electron from the bonding \(1s\sigma_g\) or anti-bonding \(1s\sigma_u\) -orbitals to the vacant \(2p\pi_g\) or \(2p\sigma_u\) orbitals (see MO-diagram below).
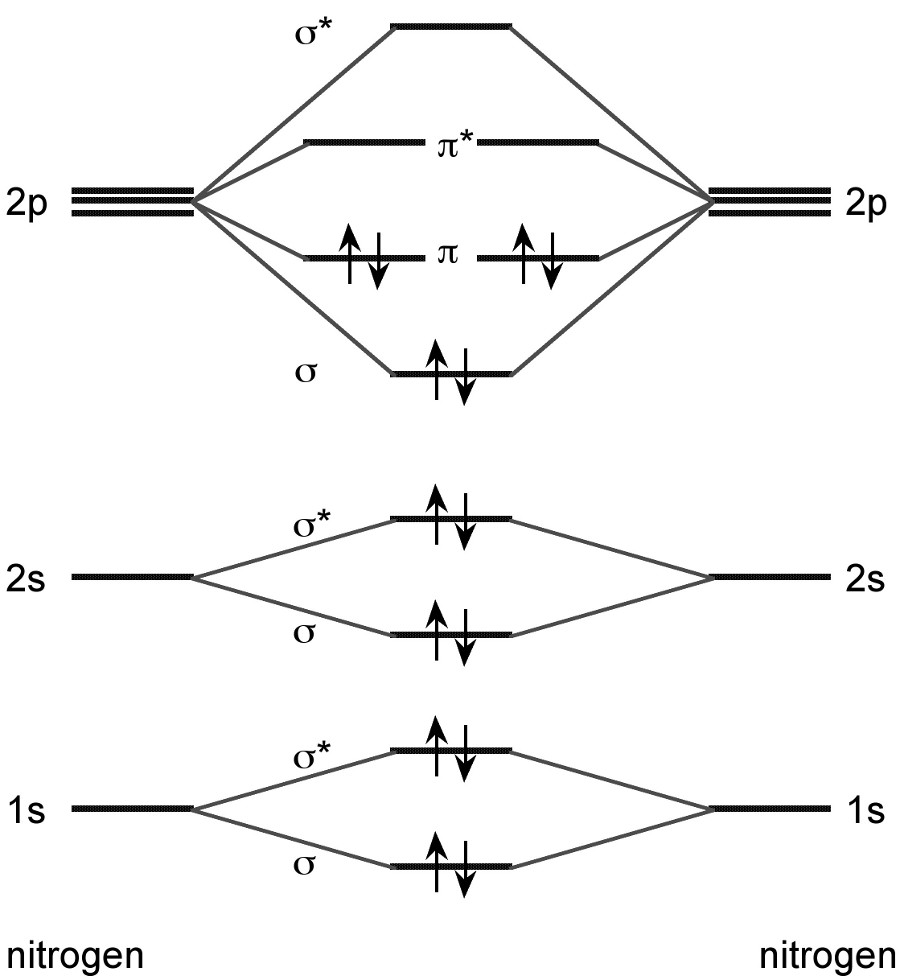
Note that this diagram does not take spin-orbit into account, but we shall consider this interaction later on. Let us first consider the possible final states. One electron leaves from one of four spin-orbitals and enters one of six spin-orbitals. This gives 24 determinants which translates into the following states:
| Configuration | States |
|---|---|
| \(1s\sigma_g^{-1}2p\pi_g\) | \(^{1,3}\Pi_g\) |
| \(1s\sigma_g^{-1}2p\sigma_u\) | \(^{1,3}\Sigma_u\) |
| \(1s\sigma_u^{-1}2p\pi_g\) | \(^{1,3}\Pi_u\) |
| \(1s\sigma_u^{-1}2p\sigma_u\) | \(^{1,3}\Sigma_g\) |
Spin-orbit free calculation¶
Preparing the input files¶
We employ the following molecular input file N2.mol
DIRAC
N2
cc-pVTZ basis
C 1 A
7. 2
N1 0.0 0.0 0.00000
N2 0.0 0.0 1.09800
LARGE BASIS cc-pVTZ
FINISH
Here we do not provide any symmetry information, meaning that we ask DIRAC to detect it. DIRAC will find that the full group is \(D_{\infty h}\). With spin-orbit coupling DIRAC will then activate linear supersymmetry, but in the spin-orbit free case it will simply use the highest Abelian single point group, that is \(D_{2h}\). For the final states DIRAC will employ the total symmetry, that is the combined spin and spatial symmetry. Here we shall keep in mind that the singlet spin function is totally symmetric (\(A_g\)), whereas the triplet spin functions transform as rotations. We know the triplet functions as:
but for our purposes it will be more convenient to form the combinations:
which transform as rotations \(R_x\left(B_{3g}\right)\) , \(R_y\left(B_{2g}\right)\) and \(R_z\left(B_{1g}\right)\) , respectively.
We can now set up the following correlation of states:
| State | Spin | Spatial | Spin \(\otimes\) Spatial |
|---|---|---|---|
| \(^1\Sigma_g\) | \(A_g\) | \(A_g\) | \(A_g\) |
| \(^1\Sigma_u\) | \(A_g\) | \(B_{1u}\) | \(B_{1u}\) |
| \(^1\Pi_{x,y;g}\) | \(A_g\) | \(B_{3g}, B_{2g}\) | \(B_{3g}, B_{2g}\) |
| \(^1\Pi_{x,y;u}\) | \(A_g\) | \(B_{3u}, B_{2u}\) | \(B_{3u}, B_{2u}\) |
| \(^3\Sigma_g\) | \(B_{3g}, B_{2g}, B_{1g}\) | \(A_g\) | \(B_{3g}, B_{2g}, B_{1g}\) |
| \(^3\Sigma_u\) | \(B_{3g}, B_{2g}, B_{1g}\) | \(B_{1u}\) | \(B_{2u}, B_{3u}, A_{u}\) |
| \(^3\Pi_{x,y;g}\) | \(B_{3g}, B_{2g}, B_{1g}\) | \(B_{3g}, B_{2g}\) | \(\left(A_g, B_{1g}, B_{2g}\right), \left(B_{1g}, A_g, B_{3g}\right)\) |
| \(^3\Pi_{x,y;u}\) | \(B_{3g}, B_{2g}, B_{1g}\) | \(B_{3u}, B_{2u}\) | \(\left(A_u, B_{1u}, B_{2u}\right), \left(B_{1u}, A_u, B_{3u}\right)\) |
Counting total symmetries we find the 24 microstates are evenly distributed amongst the eight irreps of \(D_{2h}\):
| Irrep | Core-ionized state | |
|---|---|---|
| \(A_g\) | \(^1\Sigma_g, ^{3(x)}\Pi_{x;g}, ^{3(y)}\Pi_{y;g}\) | \(x^2, y^2, z^2\) |
| \(B_{3u}\) | \(^{1}\Pi_{x;u}, ^{3(y)}\Sigma_u, ^{3(z)}\Pi_{y;u}\) | \(x\) |
| \(B_{2u}\) | \(^{1}\Pi_{y;u}, ^{3(x)}\Sigma_u, ^{3(z)}\Pi_{x;u}\) | \(y\) |
| \(B_{1g}\) | \(^{3(z)}\Sigma_g, ^{3(y)}\Pi_{x;g}, ^{3(x)}\Pi_{y;g}\) | \(xy\) |
| \(B_{1u}\) | \(^1\Sigma_u, ^{3(y)}\Pi_{x;u}, ^{3(x)}\Pi_{y;u}\) | \(z\) |
| \(B_{2g}\) | \(^{1}\Pi_{y;g}, ^{3(y)}\Sigma_g, ^{3(z)}\Pi_{x;g}\) | \(xz\) |
| \(B_{3g}\) | \(^{1}\Pi_{x;g}, ^{3(x)}\Sigma_g, ^{3(z)}\Pi_{y;g}\) | \(yz\) |
| \(A_{u}\) | \(^{3(z)}\Sigma_u, ^{3(x)}\Pi_{x;u}, ^{3(y)}\Pi_{y;u}\) | \(xyz\) |
From these considerations we now set up the following menu file for our calculation
**DIRAC
.WAVE FUNCTION
.ANALYZE
.PROPERTIES
**INTEGRALS
*READIN
.UNCONTRACT
**HAMILTONIAN
.SPINFREE
.DFT
PBE0
**WAVE FUNCTION
.SCF
*SCF
.CLOSED SHELL
6 8
**ANALYZE
.MULPOP
*MULPOP
.VECPOP
1..5
1..5
**PROPERTIES
.PRINT
1
*EXCITATION ENERGIES
.OCCUP
1
1
.EXCITATIONS !Ag
1 3
.EXCITATIONS !B3u
2 3
.EXCITATIONS !B2u
3 3
.EXCITATIONS !B1g
4 3
.EXCITATIONS !B1u
5 3
.EXCITATIONS !B2g
6 3
.EXCITATIONS !B3g
7 3
.EXCITATIONS !Au
8 3
.INTENS
0
.ANALYZE
.SKIPEP
*END OF INPUT
In the *SCF section we give the electron occupation of \(N_2\): 6 and 8 electrons in gerade and ungerade orbitals, respectively. We also ask for a Mulliken population analysis (.MULPOP) for the occupied orbitals and the orbitals involved in the core excitation.
Let us now look at how we set up the calculation of excitation energies under *EXCITATION ENERGIES. We have seen that there are three excitations per boson irrep. Note that the numbering of irreps follow what you for instance find in the \(D_{2h}\) direct product table in the output:
| | Ag B3u B2u B1g B1u B2g B3g Au
-----+----------------------------------------
Ag | Ag B3u B2u B1g B1u B2g B3g Au
B3u | B3u Ag B1g B2u B2g B1u Au B3g
B2u | B2u B1g Ag B3u B3g Au B1u B2g
B1g | B1g B2u B3u Ag Au B3g B2g B1u
B1u | B1u B2g B3g Au Ag B3u B2u B1g
B2g | B2g B1u Au B3g B3u Ag B1g B2u
B3g | B3g Au B1u B2g B2u B1g Ag B3u
Au | Au B3g B2g B1u B1g B2u B3u Ag
Note also that we skip excitations in \(B_{2u}\) and \(B_{2g}\), since they are related by symmetry to the excitations of \(B_{3u}\) and \(B_{3g}\), respectively.
If nothing further is specified the excitation energies are calculated by a “bottoms-up” approach and so we will get valence excitations only, since the core-excitations are much higher in energy. We therefore restrict the excitations to the occupied \(1s\sigma_g\) and \(1s\sigma_u\) orbitals.
We furthermore ask for transition moments to be calculated with respect to the component of the dipole moment operator. These will be non-zero only for excitations in irreps \(B_{3u}, B_{2u}\) and \(B_{1u}\). Finally we ask for analysis of what orbitals contribute to the various excitations. For this the Mulliken population analysis may come in handy as reference.
Looking at the output¶
After running the calculation, let us now look at the output. The following excitation energies were calculated
Level Rel eigenvalue Abs eigenvalue Total Energy Degeneracy
0 0.0000000000 0.000000000000 -109.506175626874 ( 1 * )
1 14.2873900530 14.287390053039 -95.218785573835 ( 2 * )
2 14.2873901429 14.287390142869 -95.218785484005 ( 2 * )
3 14.2874014745 14.287401474486 -95.218774152388 ( 2 * )
4 14.2892617095 14.289261709468 -95.216913917405 ( 2 * )
5 14.2892617988 14.289261798798 -95.216913828075 ( 2 * )
6 14.2892731363 14.289273136296 -95.216902490578 ( 2 * )
7 14.3291612539 14.329161253885 -95.177014372989 ( 2 * )
8 14.3298947237 14.329894723671 -95.176280903203 ( 2 * )
9 14.6936222414 14.693622241426 -94.812553385448 ( 1 * )
10 14.6936223755 14.693622375464 -94.812553251410 ( 2 * )
11 14.6951870758 14.695187075770 -94.810988551103 ( 1 * )
12 14.6951872031 14.695187203115 -94.810988423758 ( 2 * )
13 14.7188072608 14.718807260844 -94.787368366029 ( 1 * )
14 14.7206158042 14.720615804223 -94.785559822650 ( 1 * )
DIRAC assumes that excitation energies that are within \(10^{-9}\ E_h\) of each other come from the same degenerate state. This threshold is somewhat arbitrary and we shall see that DIRAc is not always correct.
There is sufficient symmetry in the calculation (symmetry distinct rotation) to allow DIRAC to pinpoint the symmetry of the core-ionized state and we therefore find the following distribution
Level eigenvalue (eV) Eigenvalue (cm-1) 1Ag |1B3u|1B2u|1B1g|1B1u|1B2g|1B3g|1Au |
0 0.000000000 0.000000 1| 0| 0| 0| 0| 0| 0| 0|
1 388.779649059 3135719.663853 0| 0| 0| 0| 0| 0| 0| 0|
2 388.779651503 3135719.683569 0| 0| 0| 0| 0| 0| 0| 0|
3 388.779959852 3135722.170571 0| 0| 0| 0| 0| 0| 0| 0|
4 388.830579420 3136130.444958 0| 0| 0| 0| 0| 0| 0| 0|
5 388.830581850 3136130.464564 0| 0| 0| 0| 0| 0| 0| 0|
6 388.830890359 3136132.952857 0| 0| 0| 0| 0| 0| 0| 0|
7 389.916301222 3144887.382757 0| 1| 1| 0| 0| 0| 0| 0|
8 389.936259949 3145048.360768 0| 0| 0| 0| 0| 1| 1| 0|
9 399.833788902 3224877.323614 0| 0| 0| 0| 0| 0| 0| 0|
10 399.833792549 3224877.353032 0| 0| 0| 0| 0| 0| 0| 0|
11 399.876370209 3225220.765055 0| 0| 0| 0| 0| 0| 0| 0|
12 399.876373674 3225220.793004 0| 0| 0| 0| 0| 0| 0| 0|
13 400.519108122 3230404.796465 1| 0| 0| 0| 0| 0| 0| 0|
14 400.568321089 3230801.725856 0| 0| 0| 0| 1| 0| 0| 0|
Relative real eigenvalues in other units;
Symmetry Classification in the Abelian subgroup
Level eigenvalue (eV) Eigenvalue (cm-1) 3Ag |3B3u|3B2u|3B1g|3B1u|3B2g|3B3g|3Au |
0 0.000000000 0.000000 0| 0| 0| 0| 0| 0| 0| 0|
1 388.779649059 3135719.663853 0| 1| 1| 0| 0| 0| 0| 0|
2 388.779651503 3135719.683569 0| 1| 1| 0| 0| 0| 0| 0|
3 388.779959852 3135722.170571 0| 1| 1| 0| 0| 0| 0| 0|
4 388.830579420 3136130.444958 0| 0| 0| 0| 0| 1| 1| 0|
5 388.830581850 3136130.464564 0| 0| 0| 0| 0| 1| 1| 0|
6 388.830890359 3136132.952857 0| 0| 0| 0| 0| 1| 1| 0|
7 389.916301222 3144887.382757 0| 0| 0| 0| 0| 0| 0| 0|
8 389.936259949 3145048.360768 0| 0| 0| 0| 0| 0| 0| 0|
9 399.833788902 3224877.323614 1| 0| 0| 0| 0| 0| 0| 0|
10 399.833792549 3224877.353032 2| 0| 0| 0| 0| 0| 0| 0|
11 399.876370209 3225220.765055 0| 0| 0| 0| 1| 0| 0| 0|
12 399.876373674 3225220.793004 0| 0| 0| 0| 2| 0| 0| 0|
13 400.519108122 3230404.796465 0| 0| 0| 0| 0| 0| 0| 0|
14 400.568321089 3230801.725856 0| 0| 0| 0| 0| 0| 0| 0|
The first and second block refers to singlet and triplet states, respectively. Based on the discussion in the preceeding section we see that levels 1, 2 and 3 all come from a \(^3\Pi_u\) which in \(D_{2h}\) splits into \(^3B_{2u}\) and \(^3B_{3u}\). After careful inspection we can set up the following table
| Level | eigenvalue (eV) | |
|---|---|---|
| 0 | 0.000 | \(^1\Sigma_g\) |
| 1,2,3 | 388.780 | \(^3\Pi_u\) |
| 4,5,6 | 388.831 | \(^3\Pi_g\) |
| 7 | 389.916 | \(^1\Pi_u\) |
| 8 | 389.936 | \(^1\Pi_g\) |
| 9,10 | 399.834 | \(^3\Sigma_g\) |
| 11,12 | 399.876 | \(^3\Sigma_u\) |
| 13 | 400.519 | \(^1\Sigma_g\) |
| 14 | 400.568 | \(^1\Sigma_u\) |
Looking further down in the output we find dominant inactive and virtual orbitals. Restricting attention to \(B_{3u}\) total symmetry we find that the first excited state \(^3\Pi_u\), at 388.78 eV, is dominated by the excitation 1(i:E1u) —> 4(v:E1g), which, as can be inferred from the Mulliken population analysis, corresponds to \(1s\sigma_u \rightarrow 2p\pi_{y;g}\). The second excited state \(^1\Pi_u\), at 389.91 eV, corresponds to 1(i:E1u) —> 5(v:E1g) (\(1s\sigma_u \rightarrow 2p\pi_{x;g}\)), whereas the third excited state \(^3\Sigma_u\), at 399.88 eV, is dominated by 1(i:E1g) —> 5(v:E1u) (\(1s\sigma_g \rightarrow 2p\sigma_u\)).
Within the electric dipole approximation only singlet states get oscillator strengths. In the output we find
* ISOTROPIC DL-DL OSCILLATOR STRENGTHS (f)
==========================================
DL = dipole length
Rate = Dipole radiation rate (s-1)
Lifetime = corresponding radiation lifetime (s)
Level Frequency f Rate Lifetime
------------------------------------------------------------------------
14 14.3291612539 0.11150564 0.73561E+12 0.13594E-11 1B3u
15 14.3291612539 0.11150564 0.73561E+12 0.13594E-11 1B2u
25 14.7206158042 0.00007988 0.55615E+09 0.17981E-08 1B1u
------------------------------------------------------------------------
Sum of oscillator strenghts: 0.22309
showing intensity to the \(^1\Pi_u\) and \(^1\Sigma_u\) states.
Including spin-orbit¶
Spin-orbit is included by simply commenting out the keyword .SPINFREE in the input above:
**HAMILTONIAN
!.SPINFREE
This leads to the following states:
Level Rel eigenvalue Abs eigenvalue Total Energy Degeneracy
0 0.0000000000 0.000000000000 -109.506177757989 ( 1 * )
1 14.2870674366 14.287067436576 -95.219110321412 ( 1 * )
2 14.2870902909 14.287090290867 -95.219087467121 ( 1 * )
3 14.2873870516 14.287387051622 -95.218790706367 ( 2 * )
4 14.2877107670 14.287710767041 -95.218466990947 ( 2 * )
5 14.2889390867 14.288939086714 -95.217238671275 ( 1 * )
6 14.2889619501 14.288961950065 -95.217215807924 ( 1 * )
7 14.2892586419 14.289258641924 -95.216919116065 ( 2 * )
8 14.2895824310 14.289582431019 -95.216595326970 ( 2 * )
9 14.3291623896 14.329162389555 -95.177015368434 ( 2 * )
10 14.3298959259 14.329895925905 -95.176281832084 ( 2 * )
11 14.6936210547 14.693621054697 -94.812556703291 ( 1 * )
12 14.6936211889 14.693621188921 -94.812556569068 ( 2 * )
13 14.6951858891 14.695185889130 -94.810991868859 ( 1 * )
14 14.6951860166 14.695186016639 -94.810991741349 ( 2 * )
15 14.7188060692 14.718806069152 -94.787371688837 ( 1 * )
16 14.7206146122 14.720614612164 -94.785563145825 ( 1 * )
with the following distribution on linear symmetries:
Level eigenvalue (eV) Eigenvalue (cm-1) 0g+| 0g-| 1g | 2g | 0u+| 0u-| 1u | 2u |
0 0.000000000 0.000000 1| 0| 0| 0| 0| 0| 0| 0|
1 388.770870219 3135648.857724 0| 0| 0| 0| 1| 0| 0| 0|
2 388.771492115 3135653.873661 0| 0| 0| 0| 0| 1| 0| 0|
3 388.779567386 3135719.005118 0| 0| 0| 0| 0| 0| 2| 0|
4 388.788376130 3135790.052441 0| 0| 0| 0| 0| 0| 0| 2|
5 388.821800408 3136059.637448 1| 0| 0| 0| 0| 0| 0| 0|
6 388.822422551 3136064.655374 0| 1| 0| 0| 0| 0| 0| 0|
7 388.830495947 3136129.771710 0| 0| 2| 0| 0| 0| 0| 0|
8 388.839306697 3136200.835202 0| 0| 0| 2| 0| 0| 0| 0|
9 389.916332125 3144887.632008 0| 0| 0| 0| 0| 0| 2| 0|
10 389.936292664 3145048.624628 0| 0| 2| 0| 0| 0| 0| 0|
11 399.833756609 3224877.063157 0| 1| 0| 0| 0| 0| 0| 0|
12 399.833760262 3224877.092616 0| 0| 2| 0| 0| 0| 0| 0|
13 399.876337919 3225220.504617 0| 0| 0| 0| 0| 1| 0| 0|
14 399.876341389 3225220.532602 0| 0| 0| 0| 0| 0| 2| 0|
15 400.519075694 3230404.534918 1| 0| 0| 0| 0| 0| 0| 0|
16 400.568288652 3230801.464229 0| 0| 0| 0| 1| 0| 0| 0|
Comparing with the preceeding section we see the following spin-orbit decomposition of the :math:Lambda-S` states:
| Level | eigenvalue (eV) | ||
|---|---|---|---|
| 0 | 0.000 | \(^1\Sigma^+_g\) | \(0_g^+\) (0.000) |
| 1,2,3 | 388.780 | \(^3\Pi_u\) | \(0^+_u\) (388.771), \(0^-_u\) (388.771), \(1_u\) (388.780), \(2_u\) (388.788) |
| 4,5,6 | 388.831 | \(^3\Pi_g\) | \(0^+_g\) (388.821), \(0^-_g\) (388.822), \(1_g\) (388.830), \(2_g\) (388.839) |
| 7 | 389.916 | \(^1\Pi_u\) | \(1_u\) (389.916) |
| 8 | 389.936 | \(^1\Pi_g\) | \(1_g\) (389.936) |
| 9,10 | 399.834 | \(^3\Sigma^+_g\) | \(0^-_g\) (399.834), \(1_g\) (399.834) |
| 11,12 | 399.876 | \(^3\Sigma^+_u\) | \(0^-_u\) (399.876), \(1_u\) (399.876) |
| 13 | 400.519 | \(^1\Sigma^+_g\) | \(0^+_g\) (400.519) |
| 14 | 400.568 | \(^1\Sigma^+_u\) | \(0^+_u\) (400.568) |
Note that the energies are given relative to the lowest level, that is, the ground state and that it is somewhat stabilized by spin-orbit coupling.
The effect of spin-orbit coupling shows up in the oscillator strengths:
Level Frequency f Rate Lifetime
------------------------------------------------------------------------
2 14.2870674366 0.00000008 0.52188E+06 0.19161E-05 0u+
4 14.2873870516 0.00000617 0.40461E+08 0.24715E-07 1u
5 14.2873870516 0.00000617 0.40461E+08 0.24715E-07 1u
14 14.3291623896 0.11149933 0.73557E+12 0.13595E-11 1u
15 14.3291623896 0.11149933 0.73557E+12 0.13595E-11 1u
25 14.7206146122 0.00007988 0.55616E+09 0.17981E-08 0u+
------------------------------------------------------------------------
Sum of oscillator strenghts: 0.22309
What we see is the \(0_u^+\) and \(1_u\) components of the \(^3\Pi_u\) state stealing intensity from the singlet states. This change is not very spectacular since the nitrogen molecule is composed of light atoms for which relativistic effects are not very strong. We can mimic a more strongly relativistic system by reducing the speed of light to e.g. 20 a.u.:
**GENERAL
.CVALUE
20.0D0
We now see
Level Frequency f Rate Lifetime
------------------------------------------------------------------------
2 14.7249228123 0.00019318 0.13458E+10 0.74305E-09 0u+
6 14.7354731379 0.01012800 0.70658E+11 0.14153E-10 1u
7 14.7354731379 0.01012800 0.70658E+11 0.14153E-10 1u
14 14.7841864012 0.09369466 0.65799E+12 0.15198E-11 1u
15 14.7841864012 0.09369466 0.65799E+12 0.15198E-11 1u
22 15.1211545881 0.00000251 0.18439E+08 0.54232E-07 1u
23 15.1211545881 0.00000251 0.18439E+08 0.54232E-07 1u
25 15.1494320202 0.00006483 0.47805E+09 0.20918E-08 0u+
------------------------------------------------------------------------
Sum of oscillator strenghts: 0.20791