How to visualize densities and properties¶
What we will need and cover¶
DIRAC is able to plot a variety of scalar and vector fields representing unperturbed and perturbed densities. In this tutorial we will walk through a couple of example calculations using the classic molecule benzene.
The visualization module in DIRAC always needs the unperturbed wave function, DFCOEF.
For perturbed densities, in addition to DFCOEF, we also need the perturbed “wave function” which comes out of a linear response calculation and is typically saved in a file called PAMXVC.
It is useful to perform visualization runs is 3 steps:
- Run the SCF calculation and save DFCOEF or run the response calculation and save DFCOEF and PAMXVC.
- Calculate densities using DFCOEF (and PAMXVC) and produce data files.
- Import data files to other programs (Gnuplot, Mathematica, ParaView, PyNGL, ...) to generate plots.
Note that all values (coordinates) are entered in atomic units (bohr), not in ångstrøm.
Getting the unperturbed and perturbed wave function (example molecule: benzene)¶
We will use the benzene molecule with a very poor basis set for demonstration purposes only. For production calculation this basis set is certainly not sufficient. In real life calculations the basis set needs to be well calibrated. Also the quality of the molecular structural parameters is not important here. We will call the following molecule file benzene.mol:
DIRAC
C 2 A
1. 6
H 0.000000 -2.472878 0.000000
H -2.141580 -1.236440 0.000000
H 2.141580 -1.236440 0.000000
H -2.141580 1.236440 0.000000
H 2.141580 1.236440 0.000000
H 0.000000 2.472878 0.000000
LARGE BASIS STO-3G
6. 6
C 0.000000 -1.391016 0.000000
C -1.204659 -0.695508 0.000000
C 1.204659 -0.695508 0.000000
C -1.204659 0.695508 0.000000
C 1.204659 0.695508 0.000000
C 0.000000 1.391016 0.000000
LARGE BASIS STO-3G
FINISH
The molecule is oriented in the xy-plane and later we will place the magnetic field vector along the perpendicular z-axis.
And here is a corresponding input file for the response calculation that we will call response.inp:
**DIRAC
.WAVE FUNCTION
.PROPERTIES
**HAMILTONIAN
.LVCORR
.URKBAL
**WAVE FUNCTION
.SCF
**PROPERTIES
*LINEAR RESPONSE
.A OPERATOR
'B_z oper'
ZAVECTOR
'YDIPLEN'
'XDIPLEN'
COMFACTOR
-68.517999904721
.B OPERATOR
'B_z oper'
ZAVECTOR
'YDIPLEN'
'XDIPLEN'
COMFACTOR
-68.517999904721
.ANALYZE
*END OF
Later we will want to plot the magnetically induced current density so please observe how we specify the perturbing operator for the magnetic field to be perpendicular to the molecular plane:
...
.B OPERATOR
'B_z oper'
ZAVECTOR
'YDIPLEN'
'XDIPLEN'
COMFACTOR
-68.517999904721
...
This is the operator for the magnetic field along z. If you only want to plot unperturbed densities than you can remove .PROPERTIES and everything under **PROPERTIES. Also note that in production calculation we really should run with uncontracted basis sets:
**INTEGRALS
*READIN
.UNCONTRACT
But here we will cheat and use a contracted set for speed.
Now we are ready to run the calculation (here done using MPI; finishes in ca. 10 seconds) and save the resulting DFCOEF and PAMXVC:
pam [--mpi=8] --scratch=/tmp --mw=10 --inp=response.inp --mol=benzene.mol --get="DFCOEF PAMXVC"
Verify that you have the files DFCOEF and PAMXVC in your directory, we will need them for the visualizations described further down.
You should also check that you have obtained the following response functions:
grep "at freq" response_benzene.out
<< 1, 1>>: -0.23026724E+02 a.u., E--contribution at frequency 0.0000000000 a.u.
<< 1, 1>>: 0.99833086E+02 a.u., P--contribution at frequency 0.0000000000 a.u.
76.80636218049 a.u. at frequency 0.00000000 a.u. 1.33E-06 (converged)
These are the paramagnetic (“E–contribution”), diamagnetic (“P–contribution”), and the total zz magnetizability tensor element, respectively. Of course they will have nothing to do with experimental magnetizabilities (because we use a poor basis set) but it does not matter here.
We have given the molecule without symmetry information and let DIRAC find the symmetry.
DIRAC correctly assigns the molecule symmetry but note how the molecule is reoriented:
Original Coordinates
--------------------
1 0.00000000 -4.67306218 0.00000000 1
1 -4.04699969 -2.33653298 0.00000000 1
1 4.04699969 -2.33653298 0.00000000 1
1 -4.04699969 2.33653298 0.00000000 1
1 4.04699969 2.33653298 0.00000000 1
1 0.00000000 4.67306218 0.00000000 1
6 0.00000000 -2.62863929 0.00000000 1
6 -2.27647559 -1.31431964 0.00000000 1
6 2.27647559 -1.31431964 0.00000000 1
6 -2.27647559 1.31431964 0.00000000 1
6 2.27647559 1.31431964 0.00000000 1
6 0.00000000 2.62863929 0.00000000 1
Symmetry class found: D(6h)
Centered and Rotated
--------------------
6 -1.31431964 2.27647559 0.00000000 1
6 -1.31431964 -2.27647559 0.00000000 1
6 1.31431964 2.27647559 0.00000000 1
6 1.31431964 -2.27647559 0.00000000 1
6 -2.62863929 0.00000000 0.00000000 1
6 2.62863929 0.00000000 0.00000000 1
1 -2.33653298 4.04699969 0.00000000 1
1 -2.33653298 -4.04699969 0.00000000 1
1 2.33653298 4.04699969 0.00000000 1
1 2.33653298 -4.04699969 0.00000000 1
1 -4.67306218 0.00000000 0.00000000 1
1 4.67306218 0.00000000 0.00000000 1
The following elements were found: X Y Z
It is important to remember that the “Centered and Rotated” geometry is the one that we will probe in the visualization.
Example unperturbed densities¶
Density in a plane¶
Let us plot the density in the plane spanned by the points (-8.0 -8.0 0.0), ( 8.0 -8.0 0.0), and (-8.0 8.0 0.0) with 100 steps along each side:
...
**VISUAL
.DENSITY
DFCOEF
.2D
-8.0 -8.0 0.0
8.0 -8.0 0.0
100
-8.0 8.0 0.0
100
*END OF
And copy the generated plot.2d.scalar and plot.2d.vector files back from the scratch directory:
pam --mw=10 --inp=density_2d.inp --mol=benzene.mol --put=DFCOEF --get="plot.2d.scalar plot.2d.vector"
Here we are plotting a scalar quantity so the file plot.2d.vector will contain many zeros. It is generated by default and becomes interesting for vector quantities.
Density in 3D¶
In this example we plot the density in 3D and 80 points along each direction:
...
**VISUAL
.DENSITY
DFCOEF
.3D
80 80 80
*END OF
together with the following runscript:
pam --mw=10 --inp=density_3d.inp --mol=benzene.mol --put=DFCOEF --get="plot.3d.cube plot.3d.scalar"
The generated plot.3d.cube can be used read into Molekel for instance to produce figure like this one:
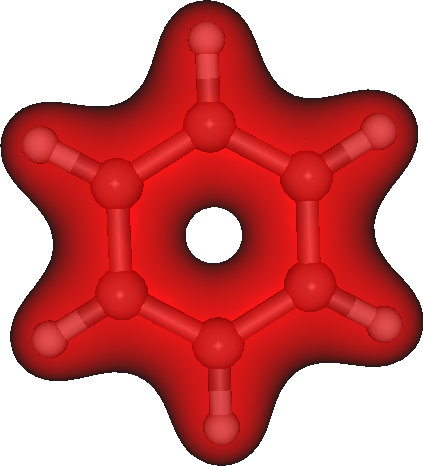
Integrating densities in 3D¶
Densities can be integrated in 3D using the numerical DFT grid. This example will integrate the unperturbed density to the number of electrons:
...
**VISUAL
.DENSITY
DFCOEF
.3D_INT
*END OF
Plotting the ELF in 3D¶
In this plot we visualize the electron localization function in benzene:
...
**VISUAL
.ELF
DFCOEF
.3D
80 80 80
.3D_ADD
10.0
*END OF
Observe how we have increased the cube size with 3D_ADD (default is 4.0 bohr):
pam --mw=10 --inp=elf_3d.inp --mol=benzene.mol --put=DFCOEF --get="plot.3d.cube plot.3d.scalar"
Here is the resulting ELF in benzene:
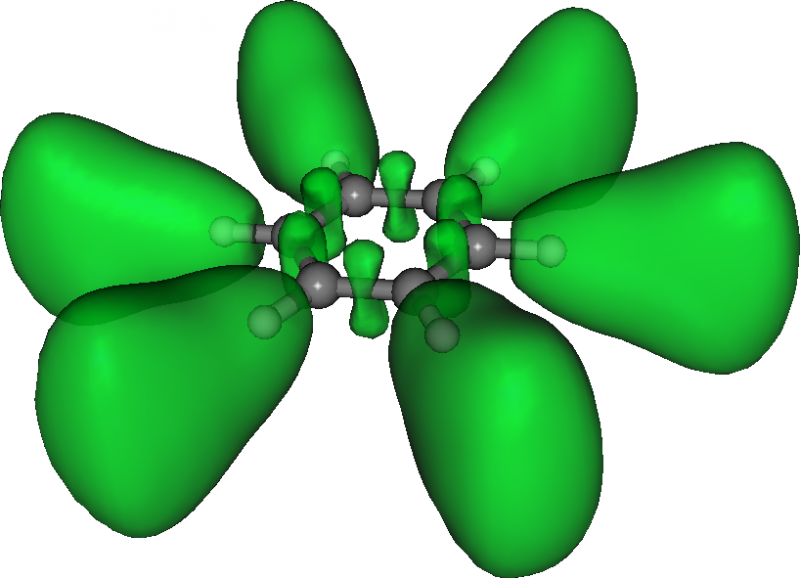
Densities and currents induced by a magnetic field¶
Current density¶
We have arrived at the heart of this tutorial: here we will calculate and plot the magnetically induced current density in benzene.
For this we will need DFCOEF and PAMXVC.
Let us first examine the PAMXVC file. For this we will use the rspread.x utility to check what is on the PAMXVC file:
./rspread.x /path/to/PAMXVC
and we get:
Solution vectors found on file : PAMXVC
** Solution vector : B_z oper Irrep: 4 Trev: -1
1 Type : E- Freq.: 0.000000 Rnorm: 0.13E-05 Length: 157
2 Type : P- Freq.: 0.000000 Rnorm: 0.13E-05 Length: 2835
In general PAMXVC can have many records. In this simple example it only contains two records: first is the “paramagnetic” response (“E-” for “electronic”), second is the “diamagnetic” response (“P-” for “positronic”).
Better names for the two records would be positive-positive energy orbital response, and positive-negative orbital response.
So, if we want to get the paramagnetic current density we will only use record 1, for the diamagnetic current density we will only use record 2, and for the total current density we will use both records.
Let’s start with the total current density. We choose a plane spanned by the points (-6.0 -6.0 0.0), ( 6.0 -6.0 0.0), and (-6.0 6.0 0.0) with 100 steps along each side (this is the molecular plane):
**DIRAC
#.WAVE FUNCTION
**HAMILTONIAN
.LVCORR
.URKBAL
**WAVE FUNCTION
.SCF
**VISUAL
.J
PAMXVC 1
.J
PAMXVC 2
.2D
-6.0 -6.0 0.0
6.0 -6.0 0.0
100
-6.0 6.0 0.0
100
*END OF
Observe how we use both PAMXVC records to get the total current density.
If we wanted to see the diamagnetic current density we would only use the record 2:
...
**VISUAL
#.J
# PAMXVC 1
.J
PAMXVC 2
With the following pam command we provide DFCOEF and PAMXVC and copy back the generated 2D plot:
pam --mw=10 --inp=j_in_plane.inp --mol=benzene.mol --put="DFCOEF PAMXVC" --get=plot.2d.vector
How about the current above the molecular plane (say, 1 bohr)? This is how it works:
...
**VISUAL
.J
PAMXVC 1
.J
PAMXVC 2
.2D
-6.0 -6.0 1.0
6.0 -6.0 1.0
100
-6.0 6.0 1.0
100
*END OF
with:
pam --mw=10 --inp=j_above_plane.inp --mol=benzene.mol --put="DFCOEF PAMXVC" --get=plot.2d.vector
The generated file plot.2d.vector contains in this case 100*100 lines with 4 numbers each: the first 2 are the position coordinates, the other 2 are projections of the vector components along these coordinates.
Integrating the current density passing through a plane¶
This is useful to get a number that can be used to quantify the aromaticity. For this molecule in the present orientation:
...
Centered and Rotated
--------------------
6 -1.31431964 2.27647559 0.00000000 1
6 -1.31431964 -2.27647559 0.00000000 1
6 1.31431964 2.27647559 0.00000000 1
6 1.31431964 -2.27647559 0.00000000 1
6 -2.62863929 0.00000000 0.00000000 1
6 2.62863929 0.00000000 0.00000000 1
1 -2.33653298 4.04699969 0.00000000 1
1 -2.33653298 -4.04699969 0.00000000 1
1 2.33653298 4.04699969 0.00000000 1
1 2.33653298 -4.04699969 0.00000000 1
1 -4.67306218 0.00000000 0.00000000 1
1 4.67306218 0.00000000 0.00000000 1
A good choice for an integration plane would be the y-z plane.
This is because in such an integration we do not want to cut through nuclear centers. Close to the nuclei the current density can be very large and non-uniform which leads to a very slow convergence with respect to the numerical grid.
In DIRAC we use the Gauss-Lobatto quadrature. You have to specify a plane, divide this plane into sufficiently many “tiles” (I would start with 5-10 tiles along each side). You also have to specify the order of the Legendre polynomial that is used to generate the roots and weights on each tile.
Let us look at an explicit example:
...
**VISUAL
.J
PAMXVC 1
.J
PAMXVC 2
.2D_INT
0.0 0.0 0.0
0.0 10.0 0.0
5
0.0 0.0 10.0
5
10
This is a plane going from the origin to 10 bohr along y and z. So it is a 10*10 bohr plane. We consider here only the region “above” the molecule. We can do this because of symmetry but have to remember to multiply the result by 2.
The plane is divided into 5 tiles along each side and the order of the Legendre polynomial is 10. To get converged results the plane has to be sufficiently large to cover “all of the current density”, with sufficiently many tiles and sufficiently high polynomial order. You have to experiment a bit.
And this is the interesting output (in atomic units):
+----------------------------------------+
! 2D Gauss-Lobatto numerical integration !
+----------------------------------------+
plane is spanned by 3 points:
"origin" 0.0000 0.0000 0.0000
"right" 0.0000 10.0000 0.0000
"top" 0.0000 0.0000 10.0000
nr of pieces to "right" 5
nr of pieces to "top" 5
order 10
scalar x-component y-component z-component
0.0000000000E+00 0.5908630369E-01 0.0000000000E+00 0.0000000000E+00
The only significant contribution is along x as it should be (due to symmetry).
If you want, you can plot and integrate at the same time by specifying a plot plane (.2D) and an integration plane (.2D_INT).
What else is there¶
Divergence of the current density:
.DIVJ
PAMXVC 1
Curl of the current density:
.ROTJ
PAMXVC 1
Spin magnetization density:
.S
PAMXVC 1
Divergence of the spin magnetization density:
.DIVS
PAMXVC 1
Curl of the spin magnetization density:
.ROTS
PAMXVC 1
Go and have fun experimenting with these!
Densities for a list of points in space¶
Let’s say that somebody asks you to verify that the density at the nuclear centers of the benzene molecule is same for all 6 centers. This is how it could be done:
...
**VISUAL
.DENSITY
DFCOEF
.LIST
6
0.000000 -1.391016 0.000000
-1.204659 -0.695508 0.000000
1.204659 -0.695508 0.000000
-1.204659 0.695508 0.000000
1.204659 0.695508 0.000000
0.000000 1.391016 0.000000
*END OF
We ask for the unperturbed density, 6 points, followed by coordinates of the 6 points.
Densities along a line¶
For example between two carbon atoms in benzene (100 steps):
...
**VISUAL
.DENSITY
DFCOEF
.LINE
-1.31431964 2.27647559 0.0
-1.31431964 -2.27647559 0.0
100
*END OF
Together with the following run script:
pam --mw=10 --inp=density_line.inp --mol=benzene.mol --put=DFCOEF --get="plot.line.scalar"
where plot.line.scalar contains tuples of 4 numbers: x-, y-, z-coordinate, and the scalar value.
For a vector density plot.line.vector contains tuples of 6 numbers: 3 for the position and 3 for the vector components.
Good practices and gotchas¶
Remember that the molecule can get reoriented if symmetry is detected automatically.
When plotting perturbed densities it is important to use DFCOEF and PAMXVC from the same run. During the visualization step the wave function should not be allowed to (re)optimize.
When plotting orbital densities it is useful to do a 3D integration (.3D_INT) at the same time. As a sanity check the integrated number should be twice the number of orbitals.
